La magia dell'interesse composto

Un fenomeno dagli effetti inconsapevolmente sottostimati che può incidere sulle nostre scelte finanziarie.

Immaginiamo di trovarci al 1^ settembre e di investire un capitale di 1 euro. Supponiamo che si tratti di un investimento magico che ogni giorno permette di raddoppiare la somma accumulata. Quindi il 2 settembre il capitale sarà cresciuto a 2 euro (1 euro di capitale iniziale più 1 euro di rendimento), il 3 settembre a 4 euro (2 euro di capitale di partenza e 2 euro di rendimento), il 4 settembre a 8 euro e così via...a quanto ammonterebbe alla fine del mese il capitale secondo questa progressione?

È la magia dell'interesse composto o della "capitalizzazione dei rendimenti", dove i guadagni maturati sono automaticamente reinvestiti e generano nuovi guadagni. Seguendo questa progressione, al 30 settembre avremo una cifra sbalorditiva che supera i cinquecento milioni di euro e che sembra superare qualsiasi nostra immaginazione.

E se invece decidessimo di beneficiare del rendimento maturato alla fine di ogni giorno ritirandolo dal conto e lasciando solo la somma inizialmente investita? quanto avremmo accumulato alla fine del mese?

Questo è il caso dell'interesse semplice. Il risultato per la nostra mente è decisamente più familiare: alla fine del mese avremo 30 euro, il capitale iniziale di 1 euro più i 29 euro ottenuti con il magico investimento (un euro al giorno per 29 giorni).

Anche per gli investimenti del mondo reale succede qualcosa di molto simile. Grazie al nostro calcolatore dell'interesse possiamo vedere come con il reinvestimento dei guadagni, cioè la legge dell'interesse composto con il fattore tempo, possa effettivamente cambiare radicalmente il risultato finale dell'investimento a parità di tasso di rendimento.

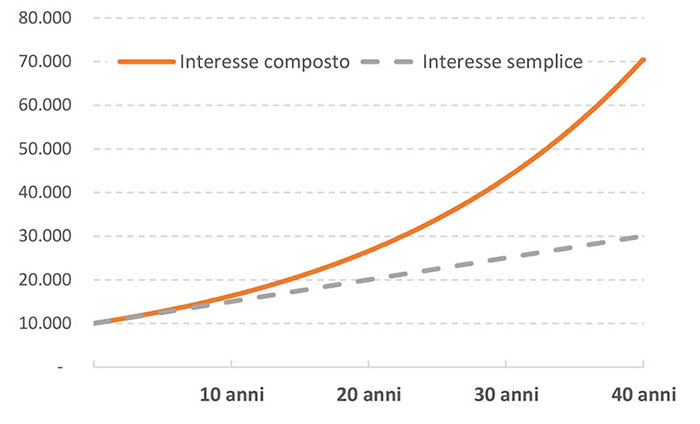
Ipotizzando, ad esempio, di investire 10.000 euro a un tasso di interesse del 5% possiamo vedere nella figura 1 come gli effetti moltiplicativi dell'interesse composto, cioè della capitalizzazione dei rendimenti, diventino via via più pronunciati all'aumentare del tempo. Dopo 40 anni avremmo a disposizione oltre 70.000 euro con l'interesse composto e "solo" 30.000 euro con l'interesse semplice.

Fig. 1

Crescita del capitale investito sotto le due ipotesi dell'interesse semplice e dell'interesse composto

(valori in euro)

"Ho fatto il mio primo investimento a 11 anni. Ho perso tempo fino ad allora"

Queste le parole con cui Warren Buffett, l'investitore più famoso e trai i più ricchi del pianeta, ci ricorda l'importanza degli effetti dell'interesse composto quando si investe per periodi lunghi. Warren Buffett non è l'investitore che ha guadagnato di più anno per anno, ma ha iniziato molto presto ad investire. Grazie alla legge degli interessi composti, ha accumulato gran parte della ricchezza, oltre il 90%, dopo i 65 anni. Oggi, a 92 anni, continua a investire!

Un cervello poco esponenziale

Come abbiamo potuto notare, si tende a sottostimare l'effetto dell'interesse composto o della capitalizzazione dei rendimenti, che avviene quando i guadagni maturati non vengono ritirati ma reinvestiti, e della crescita esponenziale del capitale che ne deriva. Questo tipo di fenomeni, infatti, hanno inizio da un livello estremamente basso e fino ad un certo punto gli effetti sembrano trascurabili per poi esplodere.

Numerosi studi hanno dimostrato la tendenza delle persone a sottostimare gli effetti della crescita esponenziale. È come se il nostro cervello si fosse evoluto per comprendere i fenomeni lineari rispetto a quelli esponenziali.

Si tratta di una vera distorsione - un bias - che, come mostrano altre ricerche, può avere un impatto importante sulla vita e sul benessere delle persone che tendono a risparmiare e a investire di meno perché ne sottostimano i benefici a lungo termine.

Pensiamo, ad esempio, a quanto sarebbe importante iniziare a risparmiare e investire anche piccole somme per la propria pensione il più presto possibile per sfruttare appieno la "magia" della capitalizzazione dei rendimenti, vista la differenza sul risultato finale che possono fare anche solo pochi anni di investimento in più. Oppure pensiamo alla tendenza delle persone a "realizzare" i guadagni, ad esempio di anno in anno, cioè a disinvestire o spendere i guadagni e ricadere così nel regime dell'interesse semplice che, come abbiamo visto, è nel lungo periodo molto penalizzante per la crescita del valore dei nostri investimenti.

Apprezzare le conseguenze della legge dell'interesse composto, sugli investimenti e sulle decisioni di indebitamento, e della crescita esponenziale del capitale o del debito che ne deriva, è una delle chiavi per una più consapevole gestione delle finanze personali.